NFA to DFA Conversion

Finite Automata (FA)

---

Finite Automata(FA) is the simplest machine to recognize patterns.

A finite automata consist of the following:

{ Q, ∑, q, F, δ }

Q : Finite set of states.

∑ : set of Input Symbols.

q : Initial state.

F : set of Final States.

δ : Transition Function.

Deterministic Finite Automata (DFA)

---

In a DFA, for a particular input character, the machine goes to one state only. A transition function is defined on every state for every input symbol. Also in DFA null (or ε) move is not allowed, i.e., DFA cannot change state without any input character.

For example, below DFA with ∑ = {0, 1} accepts all strings ending with 0.

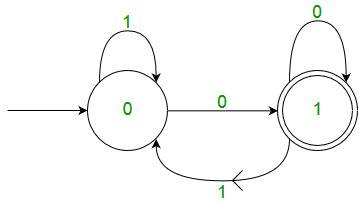
DFA consists of 5 tuples {Q, ∑, q, F, δ}.

Q : set of all states.

∑ : set of input symbols. (Symbols which machine takes as input)

q : Initial state. ( Starting state of a machine )

F : set of final state.

δ : Transition Function, defined as δ : Q X ∑ --> Q.

Nondeterministic Finite Automata (NFA)

---

NFA is similar to DFA except following additional features:

1. Null (or ε) move is allowed i.e., it can move forward without reading symbols.

2. Ability to transmit to any number of states for a particular input.

However, these above features don’t add any power to NFA. If we compare both in terms of power, both are equivalent. Due to above additional features, NFA has a different transition function, rest is same as DFA.

δ: Transition Function

δ: Q X (∑ U ϵ ) --> 2 ^ Q.

NFA to DFA Conversion Steps

---

1. Make a state table for given NFA

2. In DFA state table, initial state is same with NFA.

3. Determine all state combinations in Delta (δ = (Q X ∑)).